例题1:一直角三角形的三边分别为6,8,x,那么以x为边长的正方形的面积是多少?
分析:不要受定势思维的影响,看到6和8就认定是勾股数6,8,10,得到正方形的面积为100。此类题在没有明确直角边或斜边的时候,一定要注意分情况考虑,即分8为直角边和为斜边两种情况。因此面积可能为64+36=100,也可能为64-36=28.
例题2:如果直角三角形的两边长为3、4,则它的斜边长是多少?
分析:与例题1一样,不要看到3和4,就只想到勾股数3,4,5,还是分两种情况,斜边长是4或5。勾股数我们确实应该熟记,但是思维不应该定势。
例题3:如图,在Rt△ABC中,∠ABC=90°,AB=8,BC=6,点D为AC边上的动点,点D从点C出发,沿边CA向点A运动,当运动到点A时停止,若设点D运动的时间为t秒.点D运动的速度为每秒1个单位长度.求当t为何值时,△CBD是直角三角形,说明理由。
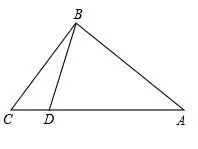
分析:分①∠CDB=90°时,利用△ABC的面积列式计算即可求出BD,然后利用勾股定理列式求解得到CD,再根据时间=路程÷速度计算;②∠CBD=90°时,点D和点A重合,然后根据时间=路程÷速度计算即可得解。
解:①当∠CDB=90°时,S△ABC=1/2ACBD=1/2ABBC,
即1/2×10BD=1/2×8×6,解得BD=4.8,
②当∠CBD=90°时,点D和点A重合,t=10÷1=10秒,
题目中如果没有明确三角形的形状,需要分情况讨论,三角形可能为锐角三角形,也可能为钝角三角形。
------文章版权归原作者所有, 未经允许请勿转载, 如有任何问题请联系我们。